A new approach known as factor investing has recently emerged in investment practice, which recommends that allocation decisions be expressed in terms of risk factors, as opposed to standard asset class decompositions. While intuitively appealing, this approach poses a major challenge, namely the choice of the meaningful factors and the corresponding investable proxies.

Simply put, factor investing proposes to regard each constituent in an investor’s portfolio, and therefore the whole portfolio, as a bundle of factor exposures. Obviously, factor models, such as those of Sharpe (1963) and Fama and French (1993), have long been used for performance measurement purposes, and several factors correspond to classical investment styles, such as value-growth investing, trend following or short volatility, that were in use in the industry before they were formally identified as asset pricing factors. In this context, the question arises as to whether factor investing is truly a new welfare-improving investment paradigm or merely another marketing fad.

A first remark is that if there are as many factors as individual securities and the factors are themselves portfolios of such securities, then thinking in terms of factors is strictly equivalent to thinking in terms of asset classes, and therefore would not add any value. More relevant is the situation where a parsimonious factor model is used, with a number of factors smaller than the number of constituents. The first challenge posed for investors who decide to express their decisions in terms of factor exposures is then the identification of meaningful factors. In this perspective, the theoretical section of recent research that we have conducted as part of the Lyxor “Risk Allocation Solutions” research chair at EDHEC-Risk Institute reviews the academic literature on asset pricing and makes a list of conditions that such factors should satisfy. We then survey a (vast) empirical literature in order to identify the most consensual factors in three major asset classes, namely stocks, bonds and commodities.

The second challenge in factor investing is the implementation of decisions in a cost-efficient way with investable proxies. On the empirical front, our paper provides an analysis of the welfare gains that can be expected from the use of proxies for factors, and discusses the choice of long-only versus long-short factors, which is relevant for many investors given that they are not allowed to take short positions.

In asset pricing theory, the relevant and important factors are the “pricing factors,” the exposures to which explain all differences in expected returns across assets.
Asset pricing theory makes a distinction between “pricing factors,” which explain differences in expected returns across assets, and “priced factors,” which earn a premium over the long run. The theory, exposed in the textbooks of Duffie (2001) and Cochrane (2005), expresses the risk premium on an asset, i.e., the expected return on this asset in excess of the risk-free rate, as a function of the covariance between the payoff and an abstract quantity known as the stochastic discount factor. The goal of theoretical and empirical asset pricing models is to find a representation for this random variable in terms of economically interpretable variables.

For instance, in consumption-based models, the stochastic discount factor is proportional to the marginal utility of consumption. This conveys an important economic intuition: risk premia exist as rewards required by investors in exchange for holding assets that have a low payoff in “bad times,” defined as times where investors’ wealth is low and marginal utility is high.

Pricing factors arise when one attempts to find observable proxies for the aggregate investor’s marginal utility. In a factor model, the risk premium on an asset is a linear combination of the factor risk premia, weighted by the betas of the asset with respect to the factor. As a consequence, all alphas are zero and the cross-sectional differences between expected returns are entirely explained by the differences in factor exposures. As for an asset, the premium of a factor is determined by its covariance with the stochastic discount factor, so that a factor deserves a positive premium if, and only if, it is high in “bad times” and low in “good times.” A factor is said to be “priced” if it has a non-zero premium. It can be shown that there is no loss of generality from searching for pricing factors among returns, but further assumptions are needed to identify their economic nature. Two main classes of theoretical models have been developed to this end. A first category uses economic equilibrium arguments. In the static Capital Asset Pricing Model (CAPM) of Sharpe (1964), the only factor, or “market factor,” is the return on aggregate wealth. The intertemporal version (ICAPM) of Merton (1973) adds as new factors the variables that predict changes in expected returns and volatilities. A second class of models refers to the Arbitrage Pricing Theory (APT) of Ross (1976) and characterizes factors as variables that explain returns from a statistical standpoint. One of the questions studied in the recent asset pricing literature is whether the factors proposed in empirical asset pricing models do meet these theoretical criteria.

The property that assets have zero alphas with respect to the factors has an interesting implication. It can be shown that a theoretical single-step solution to a mean-variance optimization problem coincides with an optimal linear combination of mean-variance efficient benchmark portfolios invested in individual securities if each individual security has a zero alpha when regressed on the benchmark portfolios. This result therefore suggests that the most meaningful way for grouping individual securities is not by forming arbitrary asset class indices, but instead by forming factor indices, that is replicating portfolios for a set of indices that can collectively be regarded as linear proxies for the unobservable stochastic discount factor, thus providing a theoretical justification for factor investing.

Empirically, the search for pricing factors in asset classes such as stocks, bonds and commodities begins with the identification of persistent and economically interpretable patterns in average returns. Recent research has subsequently started to look for multi-class factors.

While the CAPM is relatively explicit about the nature of the underlying pricing factor (the return on aggregate wealth), multi-factor models derived from the ICAPM or the APT do not provide an explicit definition of their factors. Thus, the traditional approach in empirical asset pricing has been to examine the determinants of cross-sectional differences in expected returns and to find sound economic interpretations for regular patterns (presence of a risk factor, market frictions or behavioral biases).

Most of the empirical asset pricing literature has focused on factors explaining equity returns. This literature starts in the early 1970s with empirical verifications of the CAPM and concludes that the model’s central prediction, namely the positive and linear relationship between expected excess return and the covariance with aggregate wealth, is not well validated by the data for two reasons. First, there exist patterns, or “anomalies,” that are not explained by the market exposure, and second, the relation between expected returns and the market betas is at best flat, or even negative. The most consensual patterns are those that have shown to be robust to various statistical tests, to exist in almost all international equity markets, to persist over time, in particular after their discovery, and to admit plausible economic explanations. They include the size and value effects, which are historically among the first reported anomalies: small-cap stocks tend to outperform their large-cap counterparts, and there is a positive relationship between the book-to-market ratio and future average returns. The size and value factors are used together with the market factor in the model of Fama and French (1993). Another remarkably robust pattern is the momentum effect: the winners (resp., losers) of the past three to twelve months tend to outperform (resp., underperform) over the next three to twelve months. The number of reported empirical regularities has grown fast in the recent literature, and a survey by Harvey et al. (2013) lists at least 315 of them. Among them is the controversial “low volatility puzzle,” namely the documented outperformance of low volatility stocks over high volatility stocks, the existence and persistence of which remains somewhat debated in the academic literature. Among the other noticeable patterns are the investment andprofitability effects.

In fixed-income, the two main traditional factors are term and credit. As put by Fama and French (1993), unexpected changes in interest rates and in the probability of default are “common risk factors” for bonds, so it is expected that they should be rewarded. Given that long-term bonds are more exposed to interest rate risk than short-term bills through their longer duration, one expects them to earn higher returns on average. Similarly, defaultable bonds are expected to earn a premium over default-free ones because default events are more likely to happen in bad economic conditions.

However, a mathematical decomposition of the term premium, such as those performed in the studies of bond return predictability, suggests that it varies in sign and magnitude with changes in the slope of the term structure and changes in expectations about future interest rates. Historical evidence confirms this variation. In addition to these two standard factors, recent literature has found patterns similar to those encountered in the equity class, such as momentum, value (which refers to a long-term reversal effect) and low risk.

For commodities, one can obtain a first important factor by examining the determinants of the performance of passive strategies that roll over futures contracts. Research has shown that the long-term returns to such strategies are mainly driven by the roll returns, which are the positive or negative returns earned by replacing the nearest contract with the second nearest when the former matures. Hence, the prevailing shape of the term structure of futures prices is an essential determinant of long-term returns. Specifically, backwardated futures markets (for which the term structure is decreasing) outperform contangoed futures markets (for which it is increasing). This calls for the introduction of a term structure factor defined as the excess return of backwardated contracts over contangoed contracts. A related factor is the hedging pressure, which is suggested by the eponymous theory and indirectly captures the shape of the term structure. Beyond these “fundamental” factors, a momentum factor has also been empirically reported for commodities.

A class-by-class study reveals that some patterns exist repeatedly in various classes. Asness et al. (2013) show that this is the case for short-term momentum and long-term reversal in equities, bonds, commodities and currencies. Furthermore, the single-class momentum factors are positively correlated, and the same goes for value factors. Taken together, these findings justify a new approach, which is the construction of multi-class value and momentum factors, obtained by aggregating the corresponding single-class components.

Empirical tests show that investable proxies for factors add value in single-class or multi-class portfolios when they are used as complements or substitutes for broad asset class indices. Moreover, in the equity class, a portfolio of factor indices dominates a portfolio of sector indices.

Our empirical study focuses on the following factors, which have been selected because they have well-documented historical performance, are theoretically grounded and are widely accepted by practitioners: size, value, momentum and volatility for equities; term and credit for bonds; term structure and momentum for commodities. In addition, we test multi-class value and momentum factors computed after the methodology of Asness et al. (2013). A first analysis of the descriptive statistics for these factors highlights a few simple but important facts. Each long-only factor outperforms its opposite tilt, in line with the theoretical and empirical literature, and outperforms the corresponding broad asset class index. Correlations within a class are high (above 75%), although they are lower across classes, and they are much lower for long-short versions of the factors.

The benchmark universes that we consider contain the broad indices of one or more asset class(es), which represent the market factors. For equities, we also test the benefits of using a standard sector classification, as an alternative to grouping securities according to their factor exposures. A first method for assessing the usefulness of factors is to compare the efficient frontiers in the benchmark universe and in an extended universe that also contains the factors. Formal mean-variance spanning tests (see Kan and Zhou (2012)) reject the null hypothesis that the efficient frontier of the benchmark universe is included in that of the extended universe for all long-short factors and for most long-only factors. This is first evidence that the introduction of factors improves the efficient frontier, even though these tests rely on in-sample long-short efficient frontiers, so that they may give an overly optimistic picture.

For this reason, we also conduct a series of out-of-sample tests, where we compare portfolios of traditional indices (asset class indices or equity sectors) and portfolios of factors, by imposing long-only constraints and by estimating parameters without a look-ahead bias. Since a test of the relevance of factor investing is a joint test of the relevance of the chosen factors and the chosen allocation methodology, we run the comparison for various diversification schemes that avoid the estimation of expected returns: equally-weighted, minimum variance, risk parity and “factor risk parity,” where the implicit factors extracted from the covariance matrix. The relative counterparts of these schemes, which focus on the tracking error as opposed to the absolute volatility, are also tested.

Table 1 shows a sample of results for the equity class: for most weighting schemes, the four-factor portfolios have higher average return, higher Sharpe ratio and higher information ratio compared to their ten-sector equivalents. In addition, they have a lower turnover.

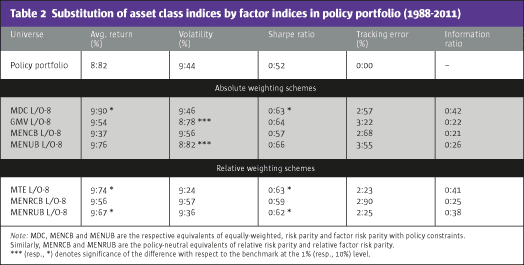
Table 2 extends the analysis to a multi-class context by comparing “policy-neutral” portfolios of equity, bond and commodity factors to a fixed-mix policy portfolio of 60% equities, 30% bonds and 10% commodities. Again, both the average return and the Sharpe ratio are improved.

As a conclusion, there exist theoretical arguments in favor of factor investing, i.e., in favor of grouping individual securities into factor indices as opposed to arbitrary forms of indices. Extensive empirical literature has documented a number of recurring patterns in the returns of equities, bonds and commodity futures, and provides investors with a rich list of insights regarding the choice of meaningful factors in each of these classes. The identification of a parsimonious set of factors capturing the largest possible number of sources of risk is an ongoing task on the academic side. On the practical side, a challenge is to develop factor indices that aim to capture factor risk premia at reasonable implementation costs. It is being addressed in the equity class with a new generation of “smart beta” indices, but similar products
are not as widely developed in other classes and no multiple-class products are available to date.

Lionel Martellini is Professor of Finance at EDHEC Business School and Scientific Director of EDHEC-Risk Institute. He has graduate degrees in economics, statistics, and mathematics, as well as a PhD in finance from the University of California at Berkeley. Lionel is a member of the editorial board of the Journal of Portfolio Management and the Journal of Alternative Investments. An expert in quantitative asset management and derivatives valuation, his work has been widely published in academic and practitioner journals.

Vincent Milhau is Deputy Scientific Director of EDHEC-Risk Institute. He holds master’s degrees in statistics (ENSAE) and financial mathematics (Université Paris VII), as well as a PhD in finance (Université de Nice-Sophia Antipolis). His research focus is on portfolio selection problems and continuous-time asset-pricing models.

References

Asness, C. S., T. J. Moskowitz, and L. H. Pedersen (2013). Value and Momentum Everywhere. Journal of Finance 68 (3), 929-985.
Cochrane, J. 2005. Asset Pricing Theory. Princeton University Press. Revised Edition.
Duffie, D. 2001. Dynamic Asset Pricing Theory. Princeton University Press, Princeton.
Fama, E. F. and K. R. French. 1993. Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics 33 (1), 3-56.
Harvey, C., Y. Liu, and H. Zhu. 2013. … and the cross-section of expected returns. Available at SSRN 2249314.
Kan, R. and G. Zhou (2012). Tests of Mean-Variance Spanning. Annals of Economics and Finance 13 (1), 139-187.
Martellini L. and V. Milhau, July 2015, Factor Investing, EDHEC-Risk Institute Publication produced as part of the Lyxor “Risk Allocation Solutions” research chair at EDHEC-Risk Institute.
Merton, R. 1973. An Intertemporal Capital Asset Pricing Model. Econometrica 41 (5), 867-887.
Ross, S. 1976. The Arbitrage Theory of Capital Asset Pricing. Journal of Economic Theory 13 (3), 341-360.
Sharpe, W. 1963. A Simplified Model for Portfolio Analysis. Management Science 9 (2), 277-293.
Sharpe, W. 1964. Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. Journal of Finance 19 (3), 425-442.