“The CBOE Volatility Index (VIX) is a key measure of market expectations of near-term volatility conveyed by S&P 500 stock index option prices. Since its introduction in 1993, VIX has been considered by many to be the world’s premier barometer of investor sentiment and market volatility.”
– Website of CBOE
Including volatility positions in an investment portfolio is donein general for portfolio diversification and for hedging purposes. The latter is true for portfolio managers that are tracking index equity portfolios and who are short volatility. When equity markets become highly volatile then the portfolio tracking error and the rebalancing costs increase but using volatility futures helps to hedge against these frictional costs. At the other extreme, the volatility futures contracts offer a direct exposure to vega with no delta involved.
Hence, speculative directional positions can be taken via VIX and VSTOXX futures. An interesting trading strategy that will be explored later on is based on the correlation between the VSTOXX and VIX. A fund manager may be long VSTOXX volatility and short VIX volatility. A similar idea is to trade on the basis between VIX and VSTOXX, given the historical evolution between the two.
The VIX index was introduced by Whaley (1993) and the methodology was further revised by CBOE in 2003. This index measures the market’s implied view of future volatility of the equity S&P 500 index, given by the current S&P 500 stock index option prices. When constructing the VIX, the put and call options are near and next-term, usually in the first and second S&P 500 contract months. “Near-term” options must have at least one week to maturity. This condition is imposed in order to minimise pricing anomalies that might appear close to expiration. When this condition is violated VIX “rolls” to the second and third S&P 500 contract months. The open interest and trading volume of VIX futures have increased rapidly over the years. As reported in Shu and Zhang (2012), shortly after launch the average open interest and trading volume was 7,000 contracts and 460 contracts,respectively. During the sub-prime crisis over the period August 2008-November 2008, the average daily trading volume was 4,800 contracts per day, and the average VIX futures price was $19.20. This implies an average daily market value of about $92 million dollars.
The EURO STOXX 50 Index is constructed from blue chip companies of sector leaders in the Eurozone: Austria, Belgium, Finland, France, Germany, Greece, Ireland, Italy, Luxembourg, the Netherlands, Portugal and Spain. The EURO STOXX 50 Volatility Index (VSTOXX) index is relatively new and provides the implied volatility given by the prices of the options with corresponding maturity, on the EURO STOXX 50 Index. By design the VSTOXX index is based on the square root of implied variance and it calibrates the volatility skew from OTM puts and calls. The VSTOXX does not measure implied volatilities of at-the-money EURO STOXX 50 options, but the implied variance across all options of a given time to expiry. This model has been jointly developed by Goldman Sachs and Deutsche Börse, such that using linear interpolation of the two nearest sub-indices, a rolling index of 30 days to expiration is calculated every five seconds using real-time EURO STOXX 50 option bid/ask quotes. The VSTOXX is calculated on the basis of eight expiry months with a maximum time to expiry of two years. If there are no such surrounding sub-indices, nearest to the time to expiry of 30 days, the VSTOXX is calculated using extrapolation, using the two nearest available indices which are as close to the time to expiry of 30 calendar days as possible. The pay-off of VSTOXX futures resembles more the pay-off of a volatility swap, being determined by the difference between the realised 30-day implied volatility and the expected 30-day implied volatility at trade initiation, times the number of contracts and the monetary size of the index multiplied (€100).
An important market change occurred on June 2009 when Eurex introduced the Mini-Futures contracts for VSTOXX, followed shortly by the ending in July 2009 of the VSTOXX futures. This important change has been motivated by the erratic volume of trading in VSTOXX futures. Hence, after this change, investors could use a volatility futures contract trading at €100 per index point rather than €1000 previously.
Thus, the Mini-Futures contracts are size-comparable with the options on VSTOXX. The minimum price change is 0.05 points which is equivalent to €5, and the contract months are the three nearest calendar months and the next quarterly month of the February, May, August, and November cycle. The evolution of the futures and mini-futures contract volume are depicted in Fig.1.
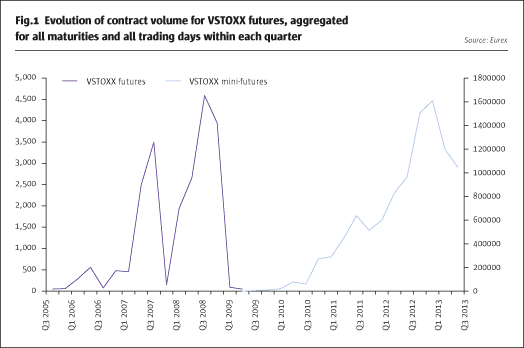
Szado (2009) and Rhoads (2011) highlighted the potential benefits of adding volatility derivatives to equity index portfolios. Changing the equity portfolio mix by adding a 10% VIX futures to the base S&P 500 portfolio would have reduced losses over the period August to December 2008 by 80% and also decreased the portfolio standard deviation by one-third. While this improvement should be expected from the design of the volatility derivatives, the impact of changing the portfolio mix by including volatility futures is unclear. Ex ante, an investor should expect an erosion of returns for portfolios including VIX futures contracts during normal time in equity markets. The opposite is expected in turbulent times.
Hence, it is unclear what an investor should expect for longer time periods. Furthermore, in the aftermath of the sub-prime liquidity crisis, other crises such as the sovereign bond crisis appeared in the European Union. It would be therefore of great interest to equity investors not only to have an updated analysis of the protective impact of VIX futures on US equity portfolios but also to know the impact of VSTOXX futures on EU equity portfolios represented by STOXX 50. Equity index returns are generally negatively skewed, while volatility futures returns exhibit positive skewness.
Statistical arbitrage strategies using GARCH forecasting
Knowing that the difference between the VIX and VSTOXX is significant and negative the following ‘naïve’ trading strategy is first investigated. A cross-country spread is entered into, short 100 VIX futures and long a number of VSTOXX futures, adjusted daily, such that the size (i.e., point value) of the short and long positions is the same. For example, given that the size of one VSTOXX mini-futures contract is €100 per point and the size of one VIX futures is $1000 per point, if the exchange rate is $1.3 for €1:
($1000/€100) / ($1.3/€1) ≈ 7.69
one would go long 7.69 VSTOXX futures contracts for each VIX contract, which gives a total position of 100 short VIX futures contracts to 769 long VSTOXX contracts. While the number of VIX contracts stays fixed at 100, the number of VSTOXX contracts is adjusted daily such that the size of both legs of the transaction matches at $100,000 per point.
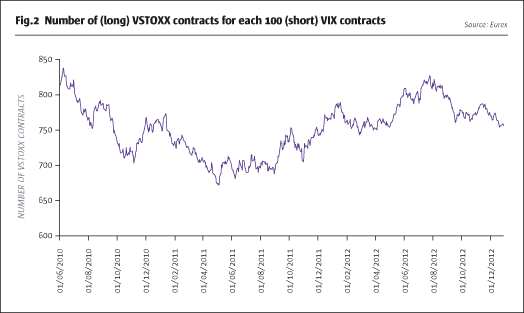
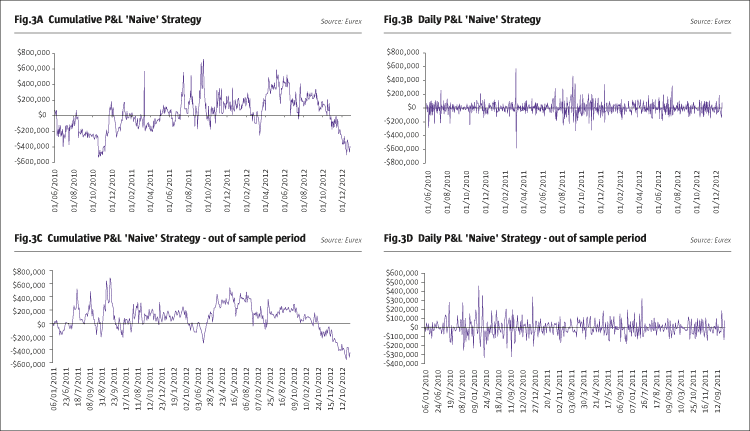
Fig.2 illustrates the evolution of the number of VSTOXX contracts from 1 June 2010 to 28 December 2012, while Fig.3A plots the cumulative profits (given in US dollars) that could have been generated by this strategy. It is of note that, if put in place at the beginning of June 2010, the strategy would have been profitable for roughly half of horizons up to 2.5 years. To make the performance of this strategy directly comparable to that of the GARCH strategy presented below, in Fig.3C and Fig.3D the cumulative and daily P&L are computed assuming the strategy commences at the start of June 2012 (rather than June 2010). This will correspond to the out-of-sample period employed for the evaluation of the GARCH strategy.
CLICK ON IMAGE TO ENLARGE
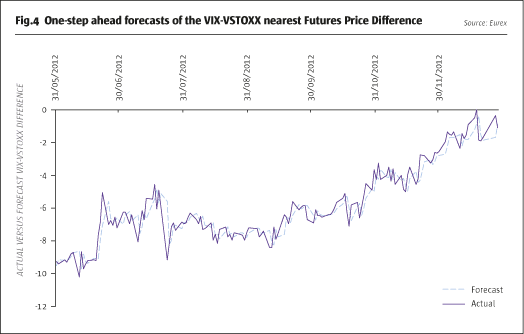
A potential application of the GARCH modelling results is for the forecasting of the VIX- VSTOXX (nearest futures price) difference which in turn can be used to inform trading strategies. Fig.4 plots the series of one-step-ahead forecasts obtained from a AR(4)-T – GARCH(1,1). The model parameters are re-estimated daily, using a rolling sample of 500 observations, with 146 observations used for out-of-sample forecasting. The results depicted in Fig.4 show that the VIX-VSTOXX (actual) futures difference remains negative for the entire forecasting period (i.e., June 2012-December 2012). This is not surprising given that during this period the European markets have been affected by the recent European sovereign debt crisis, which had a much lesser impact on the US market. Remarkably, the proposed model correctly forecasts the sign of the difference throughout the observation period.
Given that the VIX-VSTOXX futures price difference is negative throughout the forecasting evaluation period (and has a significant negative mean throughout the entire sample), the following (GARCH) strategy is proposed: we start the strategy by going long the nearest maturity VSTOXX futures, with a size equivalent to $100,000 per point and simultaneously going short 100 contracts (i.e., size $100,000 per point) of the nearest maturity VIX futures the first time our AR(4)-T-GARCH(1,1) model forecasts an increase of the spread in absolute value and unwind when the model signals a reduction in spread.
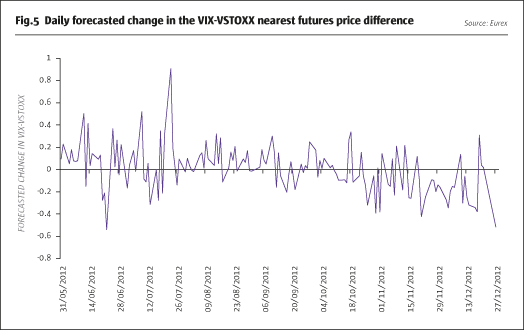
Fig.5 plots the forecasted change in the VIX-VSTOXX futures price difference, for our chosen out-of-sample period (beginning of June to end December 2012). Since the difference is negative throughout, a positive change will signify a decrease in the VIX-VSTOXX nearest futures price difference. Therefore, the strategy will be activated each time the forecasted change in the VIX-VSTOXX futures difference is negative and unwind when it is positive. More generally, one could also choose to activate or deactivate (unwind) the positions depending on whether the difference is above or below a certain threshold, which could, but need not, be equal to zero.
The performance of the trading strategy is illustrated in Fig.6, with panel a) of this figure depicting the cumulative P&L that the strategy could have generated, while the plot in panel b) is of the daily P&Ls. The results in Fig.6 are directly comparable to those in Fig.3, panels c) and d). This strategy seems to work much better, taking advantage of the excellent forecast of the spread.
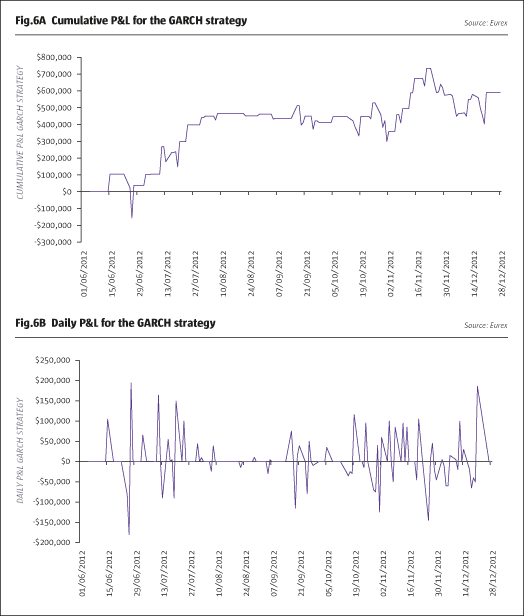
Moreover, this latter (GARCH) strategy should involve lower transaction costs as well, as the naïve strategy requires daily rebalancing of the VSTOXX leg (so that sizes of the two legs always match), whereas with the GARCH strategy one would only trade on certain days rather than every day, namely when the models signal a widening of the VIX-VSTOXX futures spread.
Conclusions
In this article, empirical evidence that adding volatility index futures to an equity and portfolio improves overall performance is brought forward. This is true for both VIX and VSTOXX. The best composition would have equity, bonds and volatility derivatives futures with first or second maturity. Using VIX and VSTOXX futures improves the return/risk profile of investment portfolios, particularly during turbulent times. Adding VIX futures contracts can improve the mean/variance investment frontier so hedge fund managers may be able to enhance their equity portfolio performance, as measured by the Sharpe ratio.
During turbulent times (such as 2008-2012), there is a great benefit in having VIX futures in the investment portfolio – the mean staying positive and Sharpe ratios at the best levels. Extreme losses can be avoided if VIX positions are added.
The second major contribution of this article is to tackle the data for US and Europe with a battery of state-of-the art GARCH models. Since the difference in VIX versus VSTOXX futures prices seems to be stationary, there is a clear incentive to identify suitable models for statistical arbitrage. Identifying a GARCH model that works well with data allows investors to engage in directional trading given by the signal produced by the GARCH model. GARCH models can be used to forecast the spread between VIX and VSTOXX futures on a daily basis and signal entering and exiting the trades. The analysis in this article shows that the statistical arbitrage approach could have provided substantial gains over recent periods.
This piece was commissioned by EUREX.
Eurex Exchange is one of the world’s leading derivatives exchanges. It offers more than 2000 products covering all major as well as alternative asset classes, all tradable on a single platform. Eurex Exchange is a member of Eurex Group.
- Explore Categories
- Commentary
- Event
- Manager Writes
- Opinion
- Profile
- Research
- Sponsored Statement
- Technical